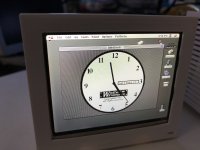
So in the 3D printed object thread, markyb86 made an excellent Quadra Pi zero case. I made a matching AppleColour RGB monitor designed to fit a small 640x480 LCD module
The module has arrived and I have made it work!
I also spent some time making a working Basilisk II image with a HyperCard clock (WildClock, it’s on archive.org if you search for it)
The “loose” wire is correcting a grounding issue which took me longer than it should have to fix.
Now I have to put it all together!


The module has arrived and I have made it work!
I also spent some time making a working Basilisk II image with a HyperCard clock (WildClock, it’s on archive.org if you search for it)
The “loose” wire is correcting a grounding issue which took me longer than it should have to fix.
Now I have to put it all together!