Testing a 6200 and comparison with 6100

[zigzagjoe]

The 040 bus clock is definitely going to be a multiple of the PPC clock... anything else makes the bus adaptation logic much more complicated than it already must be. As Phipli said apple almost certainly specified the ASIC for operation at 40mhz speeds but what configuration (ie. Programmable wait states) is required to support that remains to be seen. Again recommend referencing the memc documentation for some examples of how different DRAM grades work into 040 bus cycle timing. Something like 4-2-2-2 is more likely; 2-1-1-1 is the minimum cycle and difficult to achieve.

The 60mhz clock would be for the valkyrie private framebuffer DRAM only; that being uncoupled from the bus clock would be normal and expected. Similar to what the Epson chip on my 30video cards does, this should run as fast as practically supported by the DRAM in order to maximize bandwidth.

 

[Snial]

Hi folks,

OK, I've written the test application. It's not very big. Source code and application are included. The results take a bit of interpreting.

My PB1400c is a 603e Mac (as we all know). So, it has a 4-way x 16kB, Write-back L1 Cache. It also has a 128kB L2, Write-Through cache. So, I need to test up to "8 sets" in my test to force a flush to L2 (which also forces a flush to what's called the I/O bus on the PB5300/PB1400, which is kinda equivalent to the '040 bus on the 6200). Hence my version of the application is different to the one for the P5200/6200.

Mine's also written in CW11 Gold, I don't know how easily that converts to the later versions people tend to use. Here are my results and my interpretation of them:

Test	Ticks/Loop	Ticks	Rem	Count	Bandwidth (MB/s)
1Set	129848	93	57871	134217728	134217728*4/1048576/((93+(129848-57871)/129848)/60)=328MB/s
2Sets	129738	96	9139	134217728	134217728*4/1048576/((96+(129738-9139)/129738)/60)=317MB/s
4Sets	129421	98	95702	134217728	134217728*4/1048576/((98+(129421-95702)/129421)/60)=313MB/s
8Sets	129780	62	77761	2097152	2097152*4/1048576/((62+(129780-77761)/129780)/60)=7.69MB/s

So, what we see here is a demonstration of how great L1 cache is and the dramatic difference between L1 cache memory and the main I/O bus on a PB1400C. But are the L1 cache values realistic? Well, the PB1400c runs at 166MHz. 328MB represents 82M x 32-bit writes/s, equivalent to about 2 cycles per store instruction, which is probably correct. It also looks like there's a slight penalty for accessing different sets, which is interesting.

And my guess, is that the poor main RAM performance is because the PB1400c's bus is just 32-bits and uses pseudo-static RAM. 7.69MB/s is 1.9M 32-bit bus cycles per second for an average of 520ns per bus cycle. I mean, that's bad huh?

The version supplied will go through up to 8 sets and wait for you to press the mouse button. When you do, it'll check the Valkyrie VRAM test, writing directly, as I believe, to the VRAM addresses beginning at $F9000000. And this could be totally wrong, because for all I know those are its I/O regs so it'd be a major disaster ( @noglin ... are the I/O regs there or the screen memory itself). Perhaps I should just take the address of ScreenBits, then it would also work for my Mac. So, it's probably best to Restart the Mac instead of pressing the mouse button the first time, i.e. don't even press the mouse button once, just perform a physical Restart. The next version will have a real event loop, not a wait for Button()!.

I intend to build and submit a version that should work for the 630 at some point too. Still, this version should be useful for comparing your P6200 with my PB1400.

 

[Snial]

For your delight, I've updated the very crude app to support writing directly to the framebuffer. I did it by dereferencing the Pixmap handle from the CGrafPtr for screenbits. This version of the app should therefore work with a P6200 and if recompiled, for a P630.

Test	Ticks/Loop	Ticks	Rem	Count	Bandwidth (MB/s)
VRam	129758	60	37446	2097152	2097152*4/1048576/((60+(129758-37446)/129758)/60)=7.9MB/s

It's pretty much as slow and I'm still fairly surprised about that. The UI is still pretty awful, it does the first 4 tests and tells you to click, then it does the video test and then you need to click to finish.

68K version coming up in a few hours (it's written, but must dash).

 

[Snial]

And finally, the 68K version! These are the results I get for that:


For 68K version running on my PB1400, I get slower results.

Test	Ticks/Loop	Ticks	Rem	Count	Bandwidth (MB/s)
L1	36402	87	15562	67108864	67108864*4/1048576/((87+(36402-15562)/36402)/60)=175MB/s

I've just included the normal L1 calculation, because the other calculations that fit in cache are basically the same. It's pretty good, 175MB/s is 53% of the performance of the PPC version. I didn't optimise for 68020, because on a 68040, 68000 is probably faster and I didn't have an '040 optimisation option.

We can guess what the performance of a 6200 for the 1 and 2 sets tests will be. It ought to be simply be 75/166=148MBs, a bit slower than my 68K emulated version! The VRAM test did actually affect my screen, so I think it was a correct mapping! And it ought to be uncached too, because it's using the actual VRAM addresses.

Let me know your test results .

 

[Snial]

@Phipli , @zigzagjoe , @noglin , [at] anyone else with a 630/5200/6200 or comparable era Mac.

I've updated the tests to include RMW tests, which operate on whole words to add the current loop countdown to a given word. I think that's as valid as operating on bytes. I removed the 4 Sets test because a 603 and 603e will both flush L1 cache lines in the same way for an 8 Sets test. Here are my new PPC results:

Test	Loops/Tick	Ticks	Rem	Count	Bandwidth (MB/s)
1Set	119660	93	64898	134217728	134217728*4/1048576/((93+(119660-64898)/119660)/60)=328MB/s
2Sets	123889	96	27947	134217728	134217728*4/1048576/((96+(123889-27947)/123889)/60)=317MB/s
8Sets	123683	62	91240	2097152	134217728*4/1048576/((62+(123683-91240)/123683)/60)=313MB/s
VRAM	123997	60	39785	2097152	2097152*4/1048576/((60+(129780-39785)/129780)/60)=7.69MB/s
1SetRmw	124023	71	4461	67108864	67108864*4/1048576/((71+(124023-4461)/124023)/60)=213MB/s
2SetsRmw	123541	101	95389	67108864	67108864*4/1048576/((101+(123541-95389)/123541)/60)=151MB/s
8SetsRmw	124028	62	90206	2097152	2097152*4/1048576/((63+(124028-90206)/124028)/60)=7.59MB/s
VRAM	124008	64	664	1048576	1048576*4/1048576/((64+(124008-664)/124008)/60)=3.69MB/s

And here are the results compiled for the 68K version.

Test	Loops/Tick	Ticks	Rem	Count	Bandwidth (MB/s)
1Set	35876	88	20023	67108864	67108864*4/1048576/((88+(35876-20023)/35876)/60)=174MB/s
2Sets	35930	75	35355	67108864	67108864*4/1048576/((75+(35930-35355)/35930)/60)=205MB/s
8Sets	35888	62	27937	2097152	2097152*4/1048576/((62+(35888-27937)/35888)/60)=7.71MB/s
VRAM	35907	60	11911	2097152	2097152*4/1048576/((60+(35907-11911)/35907)/60)=7.91MB/s
1SetRmw	35920	69	20682	33554432	33554432*4/1048576/((68+(35920-20682)/35920)/60)=112MB/s
2SetsRmw	35464	72	18035	33554432	33554432*4/1048576/((72+(35464-18035)/35464)/60)=106MB/s
8SetsRmw	35738	62	27971	2097152	2097152*4/1048576/((62+(35738-27971)/35738)/60)=7.71MB/s
VRAM	35914	64	1747	1048576	1048576*4/1048576/((64+(35914-1747)/35914)/60)=3.70MB/s

As we can see, RMW performance in most cases (apart from 8Sets) is about half the speed of simply writing to memory; main memory speeds are shockingly slow; RMW for main memory, oddly enough is the same speed on my system; 68K performance is about half that of native PPC performance (impressive, and implies that the branch unit really has an effect); VRAM RMW is half the speed of VRAM Write, which is what I'd expect from the system diagram, since VRAM simply hangs off the IO bus and is directly accessed rather than going into a graphics chip buffer as you might expect for Valkyrie.

A word about the timing mechanism. I have just used TickCount() for my timings and use a simple technique to improve the timing resolution. I first time the number of simple counter loops I can do per tick; then it repeats { wait until TickCount() changes and immediate perform the test, measure the number of counter loops it can do before TickCount() changes [the remainder]; then double the number of loops in the test } until the test takes at least 1s. The synchronisation step and remainder steps give my calculations a higher resolution. The variation in the Loops/Tick represents OS overhead variations, about 1%. I run my tests with VM on as it happens. This means my timing resolution is about 0.17ms vs 17ms.

Both the PPC and 68K applications and source projects are attached. As discussed earlier, I would expect PPC6200 set tests to be 148MB/s for 1 and 2 sets, but I'm hoping the 8 sets tests will be better than 7.71MB/s. The objective really is to try and determine if the PPC6200 '040 bus speed is more likely to be 25MHz, 33MHz or 37.5MHz. This is not really possible if memory bandwidth is limited by DRAM speeds rather than the PPC/'040 bus interface. My thinking, oddly enough is that if it's 25MHz, then DRAM test performance will be comparable between the 630 and 6200 (because it's limited by the DRAM cycle time), but VRAM test performance on the 630 will be relatively better than DRAM test performance on the 6200 (because the 4 transaction buffer on Valkyrie will be limited by the bus speed rather than DRAM).

Having said that, I might need to change my tests, because my tests certainly write more than 4 transactions in one blast (they write millions). I really would want to write 4 words, then perform a long enough delay to allow a transaction buffer to clear so I'm really not testing the VRAM write performance either. Hmmm.


Let me know how the tests go for you.

 

[David Cook]

@Phipli , @zigzagjoe , @noglin , [at] anyone else with a 630/5200/6200 or comparable era Mac.

I've updated the tests to include RMW tests, which operate on whole words to add the current loop countdown to a given word. I think that's as valid as operating on bytes. I removed the 4 Sets test because a 603 and 603e will both flush L1 cache lines in the same way for an 8 Sets test. Here are my new PPC results:

Since you are trying to hammer memory as fast as possible, you should predecrement (--aCount) rather than postdecrement. This eliminates an instruction per write on the 68K.

Postdecrement



Predecrement



In fact, why not really hit it hard by subtracting 8 from the loop variable only once per loop?

 

[Snial]

Since you are trying to hammer memory as fast as possible, you should predecrement (--aCount) rather than postdecrement. This eliminates an instruction per write on the 68K.

Postdecrement

View attachment 95689

Predecrement

View attachment 95690

In fact, why not really hit it hard by subtracting 8 from the loop variable only once per loop?

View attachment 95692View attachment 95691

Of course, didn't think of that, though normally I do use --x or ++x for that reason. It's odd though, because surely a sequence like:

move.l regACount,0(a0)
subs.l #1,regACount
move.l regACount,4(a0)
subs.l #1,regACount
move.l regACount,8(a0)
subs.l #1,regACount

could be generated by a reasonable compiler?

Do you have any of these machines: P5200/P6200/P630/Q630?

 

[David Cook]

Do you have any of these machines: P5200/P6200/P630/Q630?

According to my wife, I have everything.

 

[David Cook]

could be generated by a reasonable compiler?

Yes. I completely agree that is a compiler deficiency, rather than a programmer deficiency. I notice that Metrowerks C library code differs in speed-critical sections when incrementing/decrementing pointers in PPC vs 68K. So, even they were aware that the compiler was suboptimal.

Do you have any of these machines: P5200/P6200/P630/Q630?

In all seriousness, yes, I have all but the P5200.

 

[Phipli]

In all seriousness, yes, I have all but the P5200.

A P5200 is just a P6200 with extra commitments / more baggage.

 

[David Cook]

Let me know when you've got something you want me to test.

 

[Snial]

A P5200 is just a P6200 with extra commitments / more baggage.

A P5200 is just a P6200 with more swivel. @David Cook I think the app as it currently is (or how you've modified it) is worth testing on the P6200 and P630 to see what the results are, if it's no inconvenience to get them out. Given that DRAM is so much slower than cache, I'm not yet sure how to properly distinguish the '040 bus speed in software from DRAM speeds. I'd need to write 2x or 4x 32-bits at a time instead of 8x 32-bits. One way would be to fill all the L1 cache lines, then any further write would cause a flush. Writing 4x 32-bits to Valkyrie would fill its transaction buffers and then I'd need to pause for them to empty and then repeat. So, the pause would depend upon the '040 bus speed and the Valkyrie write speed (which is also a function of the CPU clock speed).

The real question is: if the bandwidth of VRAM writes is < the bandwidth of the bus how do you estimate the bandwidth of the bus?

I think the solution is to perform 4 writes to VRAM (which depends upon the bus bandwidth) then wait long enough for the transactions to complete. For example, let's say the P6200 runs at 37.5MHz. We write 4 words, which is 2 x 64-bit words, so there's a single word write to the latches, and then the CPU bus has to wait for the '040 bus transaction to complete, then the latches can be filled with the next 64-bits and the CPU bus is free. The key thing is there is a single '040 bus transfer + a 128-bit (8-byte) transfer on the 603 bus+ a wait. This is tQw.

Similarly, if we have a 64-bit write then a pause, we incur a 0 '040 bus transfer + a 64-bit (4-byte) transfer on the 603 bus + the wait and because the burst transfers all take 1 cycle per written double-word, the 603 bus is stalled for 1 less cycle. This is tDw. tQw-tDw is the number of 603 CPU bus cycles taken for the first 2 words to be transferred on the '040 bus.

In the worst case, a 25MHz bus, each Quad word takes 5*3=15 CPU cycles, but the important bit is the first 64-bits which will take 3*3=9 CPU cycles, but I guess this would be rounded to 10 CPU Bus cycles. I don't think the 33MHz '040 bus case makes sense as it involves the '040 bus running 25/11 x slower than the CPU bus. However, the critical double-word will therefore be 3*25/11=6.818, 7 cycles, rounded to 8 cycles i.e. 4 CPU bus cycles. If the '040 bus ran at 37.5MHz, it matches the CPU bus which is neat. The critical double-word will be 3*2=6 cycles, or 3 CPU Bus cycles.

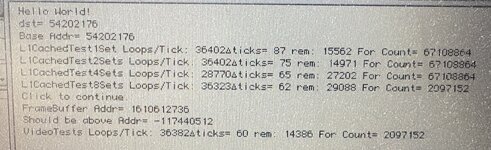
This means we need a test which can distinguish between 5, 4 and 3 CPU bus cycles over a period much longer than that. My timing mechanism is accurate to a couple of % over a 1s period. If the bandwidth for VRAM is 7.5MB/s; 1.875MW/s, that's a massive 88 cycles per word to wait, or 354 cycles for 4x long words. So, if I round to a delay of 400 nops that's probably OK.

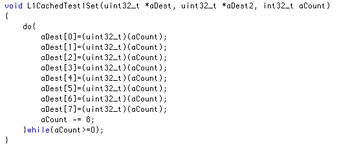
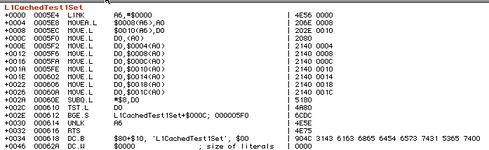
If I do 100M loops, then the difference between a single cycle will amount to a measurable amount of time at both 166MHz, 36 ticks. I just need to work out how to add a NOP in Code Warrior. Each loop is then: { Write 2 (or 4) words to non-cacheable VRAM, wait 400 nops }. This will be a PPC only test. Thank goodness I'm not making assumptions within this test !